Veri analizinin ilk aşamalarından biri verinin konum parametrelerini tespit etmektir. Konum parametreleri arasında ortalamalar ilk akla gelen ve en çok kullanılan istatistiklerden biridir.

Ortalamalar hesaplama itibariyle oldukça basit görünseler de oldukça hassas istatistikler olabilirler. Özellikle aykırı değerlerin varlığı halinde, ortalamalar verinin merkezi eğilimini doğru şekilde yansıtmayabilirler. Bu nedenle verinin içeriğine göre doğru ortalamanın alınması önem kazanmaktadır.

Örneğin, aşağıdaki 20 gözlemlik veri setini ele alalım

27	24	30	24	32	-49	28	20	45	-21
26	22	24	25	21	46	23	28	29	16

Yukarıdaki verinin aritmetik ortalaması 21’dir. Çarpıklık değeri (verinin normal dağılıma sahip olup olmadığının bir ölçütü) ise -13,5 olup negatif çarpıktır. Yani veri normal dağılıma sahip değildir.

Verinin normal dağılıma sahip olmamasının sebebi içinde bulunan aykırı değerlerdir. Aşağıdaki Q-Q plot ve kutu grafiğini inceleyelim.

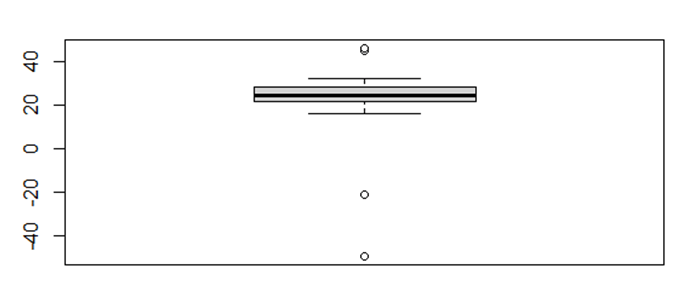
Q-Q grafikte kırmızı doğru üzerinde yer almayan noktalar, normal dağılımı bozan aykırı değerlerdir. Altındaki kutu grafiği de aynı aykırı değerlerin varlığını bize göstermektedir.

Bu sebeple normal dağılıma sahip olmayan bu veride konum parametresi tespiti yaparken aritmetik ortalamayı kullanmak doğru değildir. Sebebi ise veride aykırı değerler bulunmasıdır. Aritmetik ortalamanın güvenle kullanılabilmesi için söz konusu bu aykırı değerler çıkartılmalıdır.

Bu tür durumlarda, bir diğer yaklaşım ise veriden herhangi bir değer çıkartmak yerine aykırı değerlerden etkilenmeyen konum parametre tahmin edicileri kullanmaktır. Bunlardan en çok kullanılanlarından biri Budanmış Ortalama (Trimmed Mean) değeridir. Bu yöntemde küçükten büyüğe doğru sıraya dizilmiş veri değerleri başından ve sonundan belirli bir oranda kesilir (budanır). Uygulamada genellikle budanma oranı α=%10 olarak kullanılır. Aşağıdaki formülden yararlanılır.

Veriden aykırı değerleri elimine etmek için baştan ve sondan %10 ve %20 kesilince; yani budanınca ortalamalar aşağıdaki gibi değişmektedir.

T(α=0.10) = 24.93     T(α=0.20) = 25.08

Verinin %10 budanmış ortalaması 24.93 olarak hesaplanırken; bu değer %20’lik budanmış ortalama için 25.08 olarak düzelmiştir. Budanmış ortalamalar bu örnekte bize daha doğru sonuçlar vermiştir. İlk başta hesapladığımız aritmetik ortalama ile karşılaştırıldığında ortaya çıkan bu sonuçlar tıp, mühendislik ve sosyal bilimler gibi birçok alanda önemli bir fark olabilmekte, daha fazla gözlem sayısı veya aykırı değer içeren veri setleri için daha büyük farklar ortaya çıkmaktadır.

Bunun dışında, konum parametresinin aykırı değerlerden etkilenmediği Trimean ve genişletilmiş medyan gibi farklı istatistikler de uygulamada kullanılmaktadır.